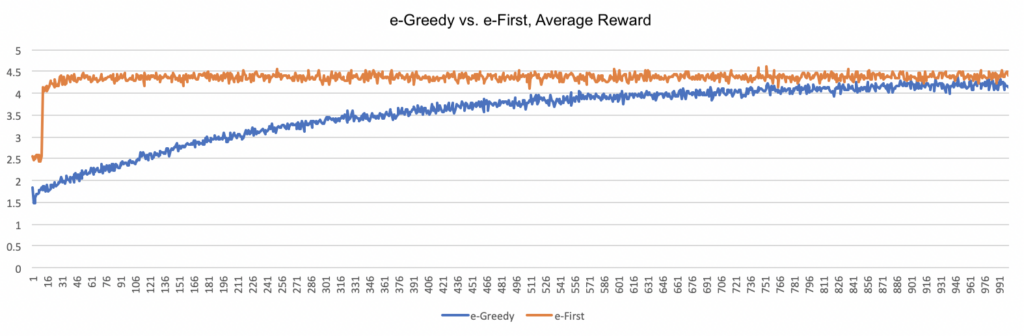
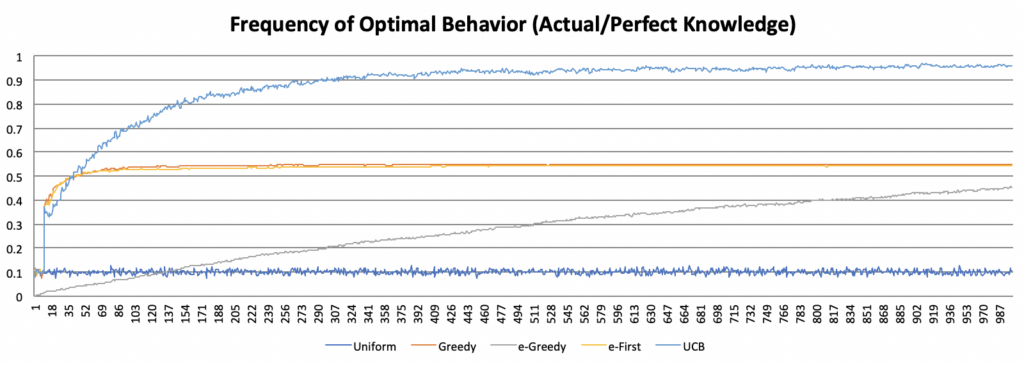
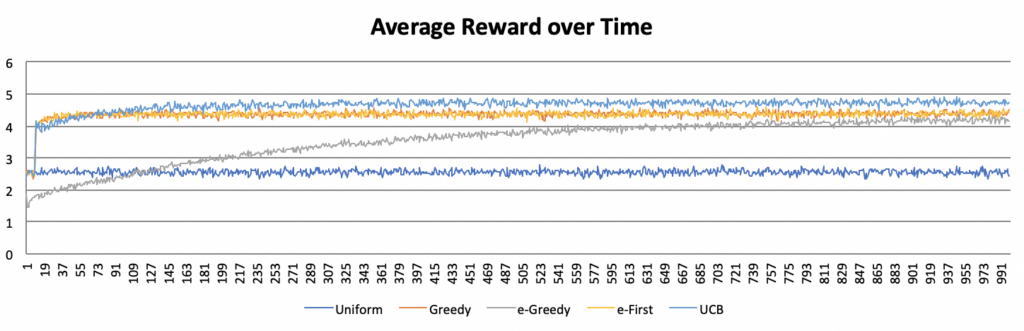
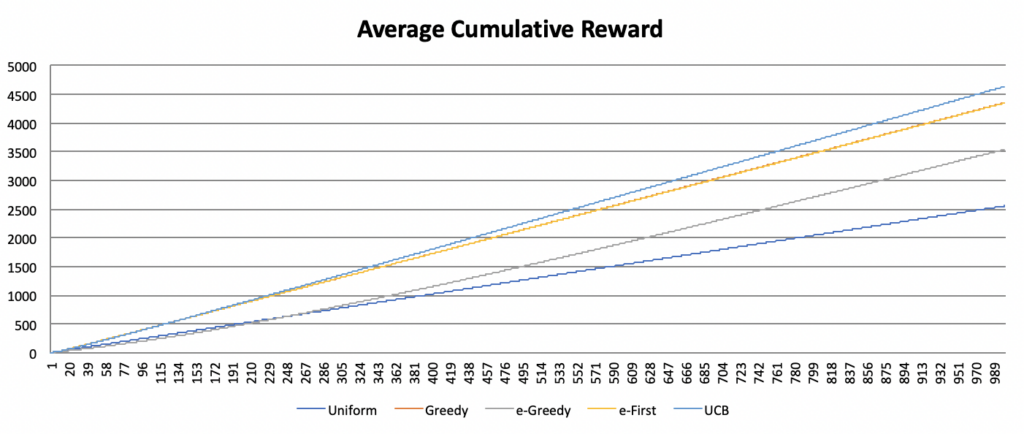
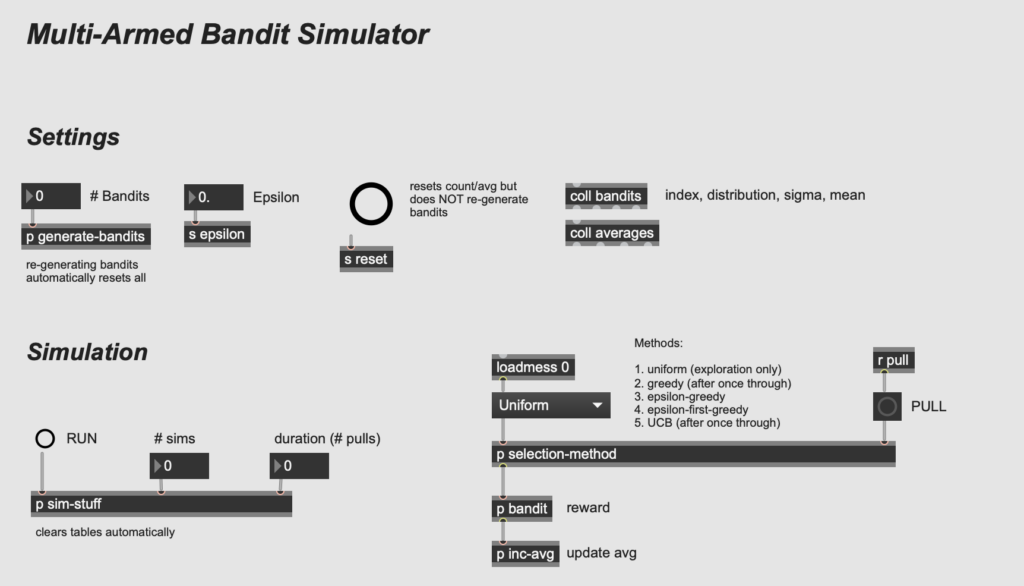
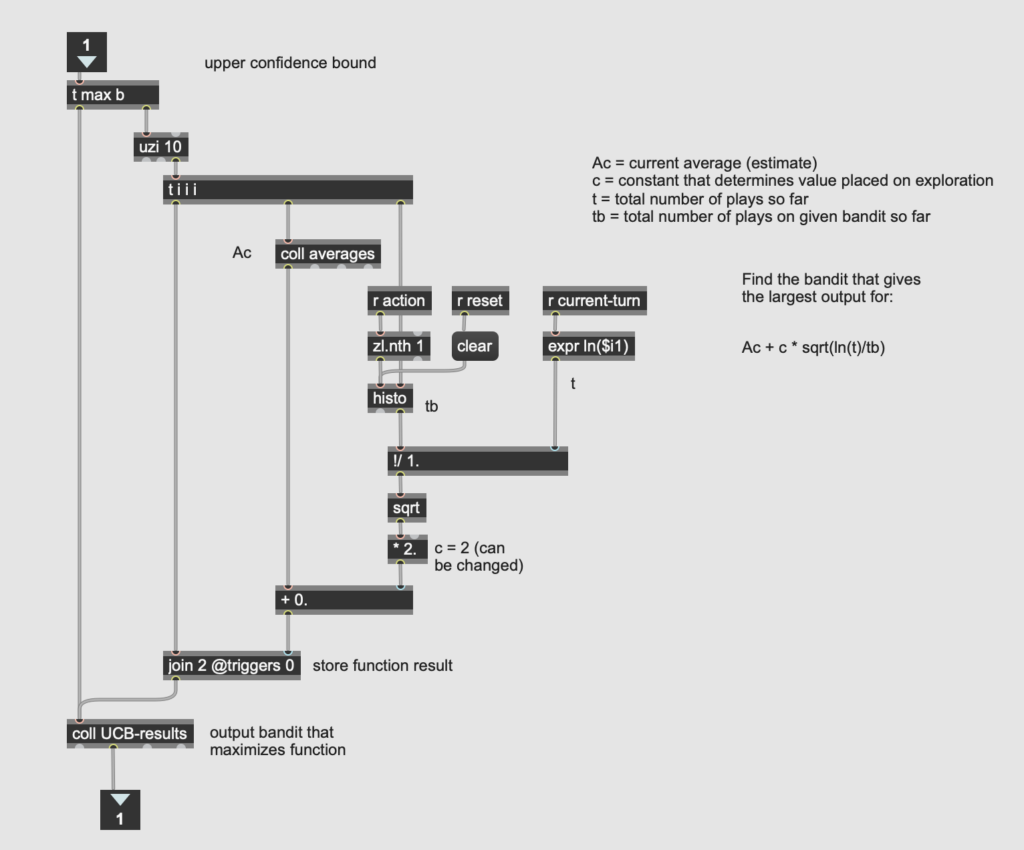
In this post, I want to discuss a slightly different usage for neural networks than has been explored so far. Rather than using neural nets to define relationships between strictly musical data (as in the previous post), here I will use them to define relationships between gestures and sounds.
Gesture recognition—the interpretation of human gestures by computers—is an important topic for the application of machine learning methods. Of course, what constitutes a “gesture” can vary widely depending on the context. In this post, I’ll be imagining the movement of a hand, fingertip, or other single point in a vertically oriented, two-dimensional plane. (Imagine tracing a shape on a steamed-up bathroom mirror.)
Just as in the previous post, I’ll use the ml.star library for Max developed by Benjamin Day Smith. You can download it through the Package Manager (File -> Show Package Manager). As before, we’ll also use a simple type of neural network called a multilayer perceptron (mlp), represented by the object [ml.mlp].
The basic idea for this patch is that each gesture will be represented as a list of numbers. When training the neural net, the user will specify a gesture label, which will then be associated with the particular sequence. I will use eight distinct labels, though this is easily modifiable. Over time, the idea is that the neural net can generalize what is distinctive about each gesture. Once the training is complete, the neural net will be able to categorize new gestures by assigning labels to the new gestures.
There are many different ways of defining gestures. For example, gestures can be dynamic (moving) or static (not moving). I’m especially interested in dynamic gestures, since their beginnings and endings can be recognized to automatically tell the computer when a gesture is starting or ending. To keep things simple, I will divide up the two-dimensional plane into eight columns and characterize each gesture according to the average values in these columns. (The fact that I have eight labels and eight columns is entirely coincidental—these do not have to be the same number.) The user will sweep their hand back and forth across the plane horizontally, with the variation in vertical position defining each gesture.
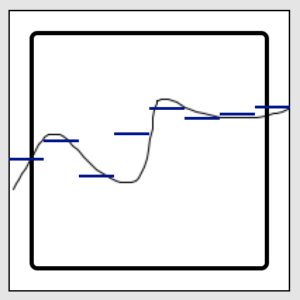
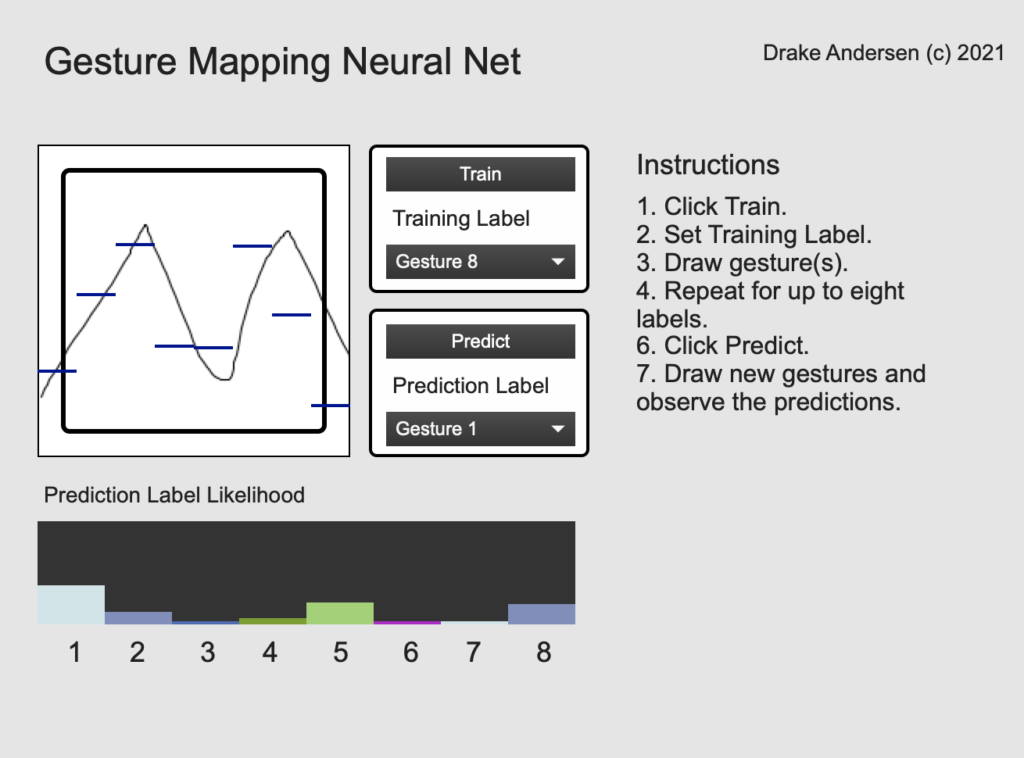
The image above illustrates a typical gesture, with the continuous human-generated gesture given by the black line, and the mean-based simplification given by the eight blue bars. (There is a slight horizontal discrepancy between the display position of the bars and the data segments they represent.)
Gesture recognition typically involves a lot of pre-processing because you have to transform human gestures—which are typically complex and time-based—into an input format that a neural network can recognize and work with. In this case, the eight vertical columns are the eight data points that make up the input layer of the neural network. The output layer will have eight points as well, but these will represent the eight possible gesture categories. These categories, it should be emphasized, will be completely user-defined: whatever the user labels “Gesture 1” will become gesture 1, etc.
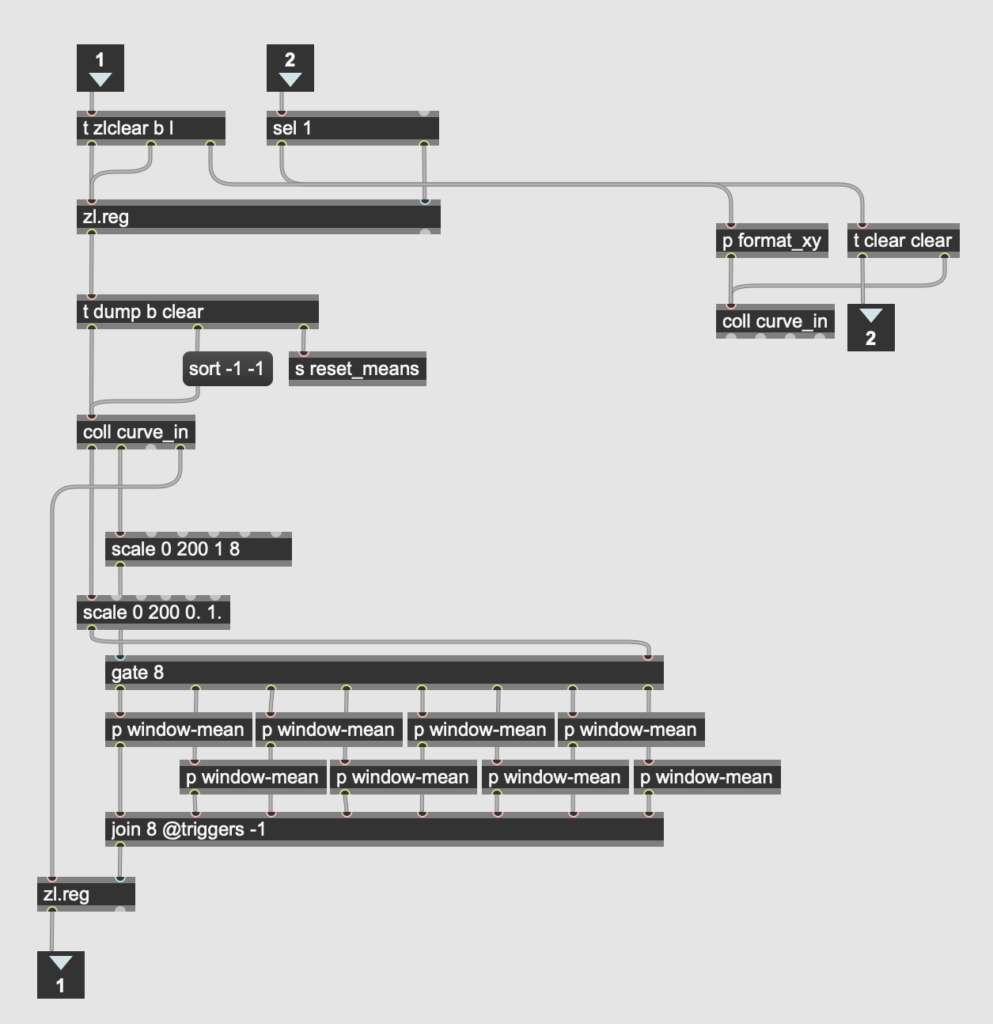
There were a handful of other minor processing details. For example, the [lcd] object used for drawing the line counts y values from the top down. In order to not confuse myself, I flipped this by running the xy coordinate list output through a [vexpr] object with a simple expression. I also had to calculate the mean of each segment separately, which involved sorting the values from the “dump” output of the coll object storing the line’s coordinates into eight bins of equal size. I ended up solving this in reasonably elegant fashion by scaling the x values to the range of one to eight and using them as the control for an 8-outlet gate, with each output leading to a separate [mean] object.
When in prediction mode, the patch gives not only the most likely label for a gesture, but also the likelihood for each label (as a multicolored [multislider] object). The final version of this patch, while functional and easy to use, also has plenty of room for improvement. For example, the inner workings of the neural net remain hidden to the user so as not to clutter the interface, but this also prevents the user from adjusting the inner structure to produce better predictions. The patch would also benefit from some gesture “filtering,” by which gestures are not recognized unless they pass across all eight columns. This will become especially important when we link it up with a computer vision system such as the LEAP motion in a later post.