This is the first entry in a series of posts dedicated to implementing reinforcement leaning algorithms in Max. Reinforcement learning is an area of machine learning I have not previously explored, so these posts will serve as both tutorials and as a way of tracking my own progress.
The idea of using a reinforcement learning strategy for a music-related machine learning project was first suggested to me by a colleague, Daniel Fox. Since it was a new area for me, I started out by doing some research. I found this library for Max, but I ultimately decided to implement the algorithms directly myself. A few especially helpful resources when getting started included:
- Reinforcement Learning: An Introduction, 2nd ed. by Richard S. Sutton and Andrew G. Barto
- David Silver’s introductory video series
- Statquest’s videos on gradient descent
I started out by looking at the first couple of chapters of the Sutton/Barto. I decided to begin by building a patch that could simulate a multi-armed bandit problem, since that is the problem that begins the book. A multi-armed bandit problem is a category of problem in which one is presented with a number of different options, each of which is associated with some kind of reward. The user (“the agent”) attempts to maximize the rewards gained by employing various strategies.
At the core of these problems is a tradeoff between exploration (trying unknown options) and exploitation (repeatedly making the same choice when a high reward is received). The term “multi-armed bandit” refers to a hypothetical instance of the problem in which one chooses between many different slot machines, each with different payout (reward) distributions. In this metaphor, if the agent explores too little, they may miss out on the highest-paying machine; if they explore too much, they lower their overall reward by wasting time on the low-paying machines.
As I began to read up on this problem, it became clear that I would have to lay groundwork in three major areas: (1) conceptual framing and goals; (2) mathematics; and (3) technical implementation in Max. Of the three, working out the math (and brushing off my calculus) was definitely the most difficult.
At the core of the algorithms described in the second chapter of the Sutton/Barto was the need to keep a running tally of actions taken and rewards received. This is critical for maintaining a running average for each machine, which allows the agent to determine which machine has the best payouts at each moment.
Yet as the authors point out, over the long run this approach is not computationally efficient. Instead, they introduce a formula for incrementally calculating a running average (see section 2.4), where the average is continually adjusted with each new reward, and previous rewards do not need to be stored. I found their explanation a little confusing at first, but this blog post helped clarify the formula for me. My implementation is saved as inc_avg_demo.maxpat in the download bundle.
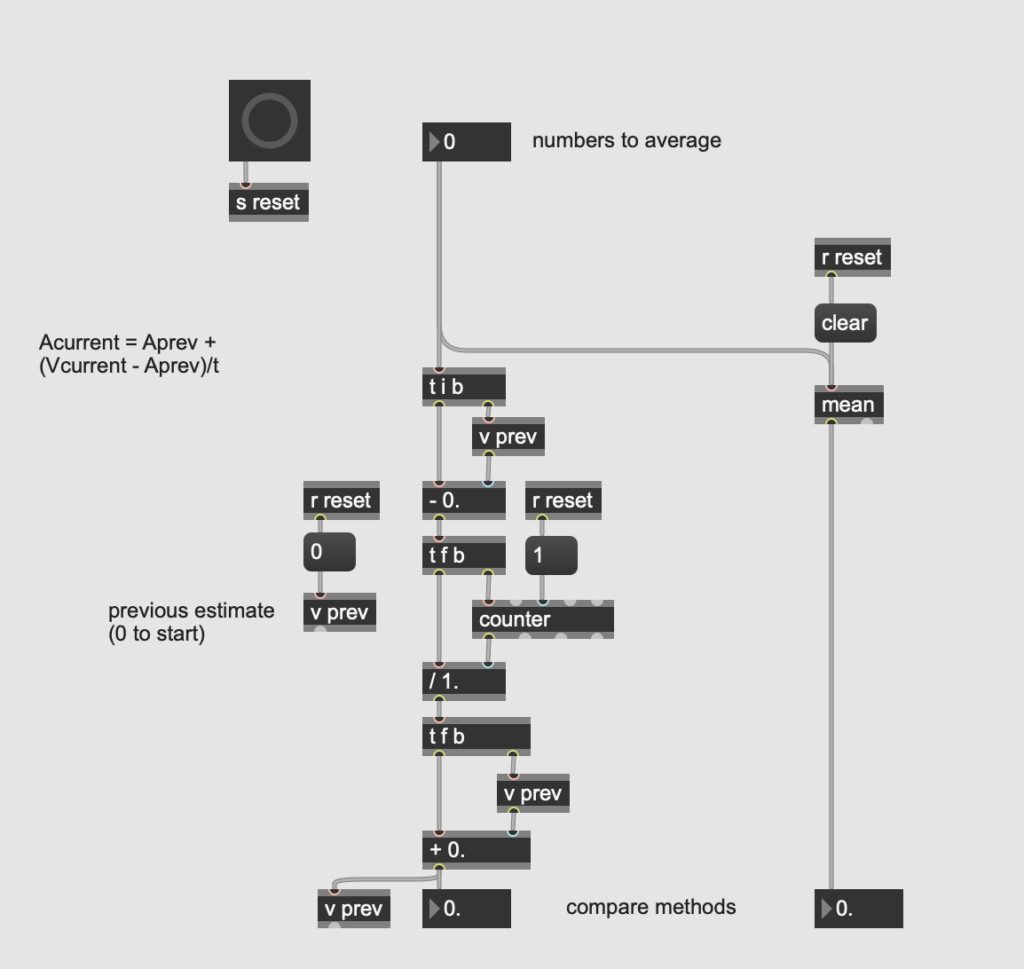
My patch allows you to compare the incremental calculation with the results from the [mean] object. While similar in function, the [mean] object is not optimal for this application because I have to calculate an average for each of an arbitrary number of bandits. This would require an arbitrary number of [mean] objects or perpetual storage of all previous values to swap in and out (a data set that increases without limit is precisely the kind of thing we want to avoid!). My implementation can be used for multiple bandits with finite data/computation by saving the running average for each, labeling the bandit number, and using [histo], [counter] or similar to keep track of how often a given bandit has been used.
A second issue that arose was the need for random number generation following a particular distribution. While not strictly necessary, using a Gaussian (rather than uniform) distribution allowed me to more closely compare my results with those in the book. I used the [randdist] object from the CNMAT externals package (download via the Package Manager in Max).
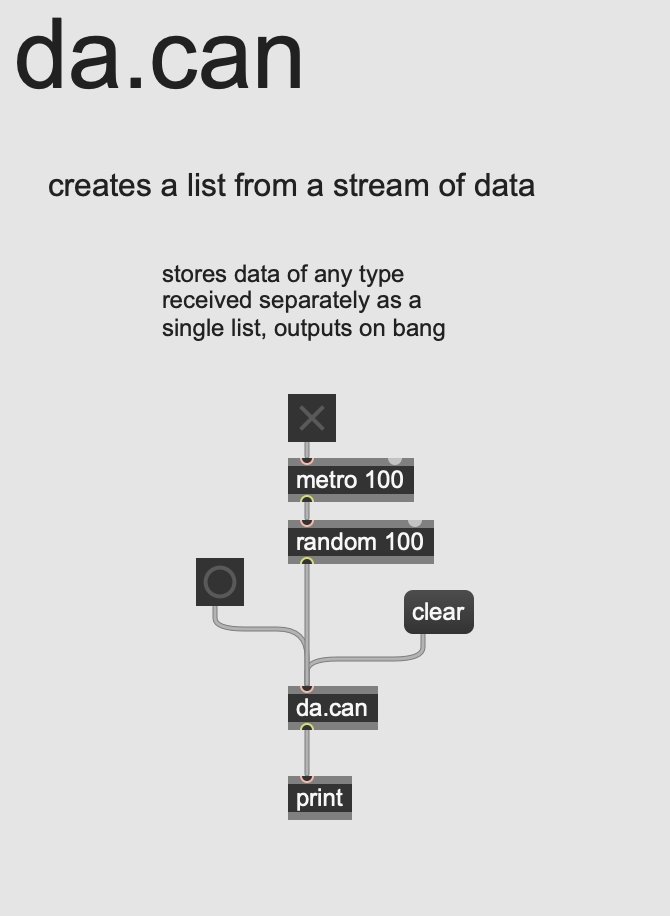
The third issue—and the last I’ll discuss in this post—to arise in these early stages was more of a technical concern than a mathematical one. I needed to be able to receive a stream of separated data (of arbitrary length) and output it as a single list. There’s not a Max object that precisely does this: zl.group requires a number to be specified in advance, and zl.reg needs everything at once. (Incidentally, the bach.collect object does this quite nicely, but I didn’t want to invoke bach for a single operation.) I ended up creating an abstraction I call da.can (like a can, you fill it up and then dump it out) that assembles anything it receives into a list, outputs with bang, and resets with a clear message. It’s part of the collection I store here.
In my next post, I’ll share my multi-armed bandit simulator patch, which allows you to test and compare different algorithms for maximizing rewards.